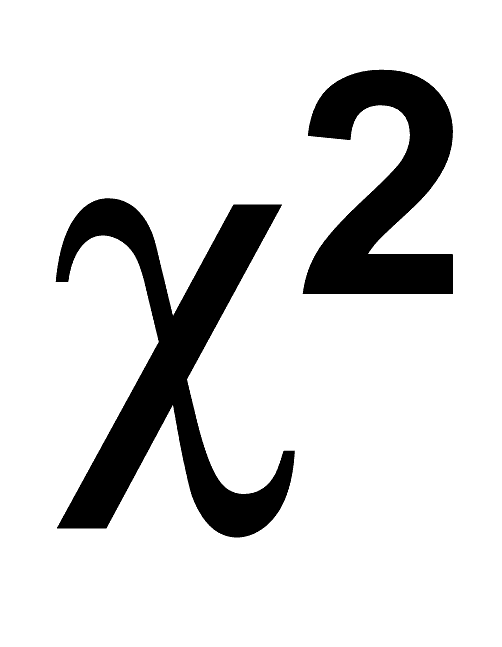The squared symbol, often represented as a small 2 placed slightly above the right of a number, holds a significant place in mathematics and various scientific fields. It is a powerful tool that allows mathematicians, scientists, and students to express the concept of squaring a number succinctly. Whether you're calculating the area of a square, working with quadratic equations, or exploring more complex mathematical theories, the squared symbol is essential in simplifying expressions and making computations more manageable. The versatility of this symbol extends beyond mathematics, influencing various disciplines such as physics, engineering, and even computer science.
The use of the squared symbol is not limited to academic settings; it has practical applications in everyday life. From calculating the area of a room to determining the amount of paint needed for a wall, understanding how to use the squared symbol can enhance problem-solving skills. Furthermore, as technology continues to advance, the squared symbol remains relevant in programming and algorithm development, showcasing its enduring importance in both theoretical and applied mathematics.
In this article, we will delve deeper into the squared symbol, exploring its historical background, mathematical significance, and real-world applications. We will also answer common questions surrounding its use and provide examples to illustrate its importance in various contexts. Whether you are a student, educator, or simply a curious individual, this comprehensive guide will enhance your understanding of the squared symbol and its multifaceted roles.
What is the Squared Symbol?
The squared symbol (²) is a mathematical notation that indicates the operation of raising a number to the power of two. In simple terms, squaring a number means multiplying that number by itself. For instance, if we take the number 3 and square it, we would write it as 3², which equals 9. The squared symbol is widely used in various branches of mathematics, including algebra, geometry, and calculus, to express quadratic relationships and functions.
How Did the Squared Symbol Come into Existence?
The history of the squared symbol can be traced back to ancient civilizations, where mathematicians began to understand the concept of area and geometric shapes. The use of symbols to represent mathematical operations evolved over time, with the squared symbol being formalized in the 17th century by mathematicians such as René Descartes and John Napier. As mathematical notation became more standardized, the squared symbol gained popularity in textbooks and academic literature, paving the way for its widespread use in modern mathematics.
Why is the Squared Symbol Important in Mathematics?
The squared symbol plays a crucial role in mathematics for several reasons:
- Expressing Area: The squared symbol is essential for calculating the area of square-shaped objects, where the area is defined as the length of one side squared.
- Quadratic Functions: In algebra, quadratic equations often involve terms with squared variables, making the squared symbol fundamental for solving these equations.
- Distance Calculations: In geometry and physics, the squared symbol is used in formulas to calculate distances, such as the Pythagorean theorem.
- Statistics: The squared symbol is also employed in statistical formulas, such as the variance, where the differences from the mean are squared.
How is the Squared Symbol Used in Real Life?
The application of the squared symbol extends beyond theoretical mathematics into various real-life scenarios. Here are some practical uses:
- Architecture: Architects use the squared symbol to calculate the area of plots and structures, ensuring efficient use of space.
- Engineering: Engineers apply the squared symbol in design calculations to determine load-bearing capacities and material requirements.
- Finance: In finance, the squared symbol may be used in models that predict returns on investments where growth is compounded.
- Sports: Coaches and analysts use squared formulas to calculate statistics and performance metrics for athletes.
What Are Some Common Misconceptions About the Squared Symbol?
Despite its widespread use, there are some common misconceptions about the squared symbol:
- Only for Whole Numbers: Many believe that the squared symbol can only be used with whole numbers; however, it can be applied to fractions, decimals, and even negative numbers.
- Only for Area Calculations: While the squared symbol is often associated with area, it is also critical in various mathematical equations and functions.
- Understanding Power Notation: Some may confuse the squared symbol with other power notations; it's important to understand that squaring is specifically raising a number to the power of two.
How Can One Master the Use of the Squared Symbol?
Mastering the use of the squared symbol requires practice and a solid understanding of the underlying mathematical principles. Here are some tips to enhance your skills:
- Practice Regularly: Solve various mathematical problems that involve squaring numbers to build confidence.
- Visual Learning: Utilize visual aids, such as graphs and diagrams, to better understand how the squared symbol relates to geometric shapes.
- Engage with Educational Resources: Use online tutorials, textbooks, and videos that cover the concept of squaring numbers and its applications.
- Collaborate with Peers: Discuss mathematical concepts with classmates or study groups to gain different perspectives and insights.
Conclusion: The Enduring Relevance of the Squared Symbol
The squared symbol is a fundamental component of mathematics that transcends its simplistic appearance. Its applications are vast and vital, influencing numerous fields and everyday situations. By understanding the significance and utility of the squared symbol, individuals can enhance their mathematical literacy and problem-solving capabilities. Whether you're a student tackling algebra or a professional working on complex engineering designs, the squared symbol will continue to be an invaluable tool in your mathematical toolbox.