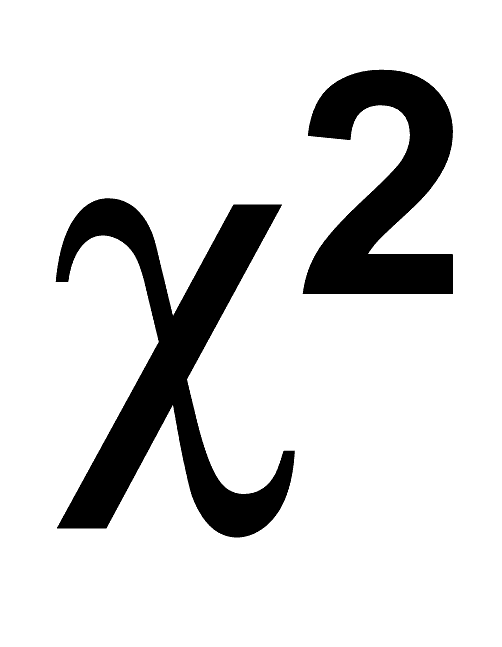Mathematics is a fascinating realm, filled with numbers and operations that hold deeper meanings and applications in our daily lives. One such concept is the idea of "squared," which refers to the multiplication of a number by itself. When we talk about "2 squared," we delve into the world of exponents, where we explore how this operation can be applied in various mathematical contexts. As we embark on this journey, we'll uncover the significance of squaring numbers and how it relates to other mathematical principles. The term "squared" may sound simple, yet it opens the door to a multitude of concepts that are foundational in mathematics.
In essence, when we say "2 squared," we are referring to the calculation of 2 multiplied by itself, which results in 4. This operation not only serves to enhance our understanding of basic arithmetic but also plays a crucial role in more complex mathematical functions. The implications of squaring a number extend to geometry, algebra, and even real-world applications, showcasing the versatility of this mathematical operation.
Throughout this article, we will answer common questions about "2 squared," including its applications in various fields, its historical context, and its relevance in everyday life. Whether you're a student seeking clarity or a math enthusiast looking to deepen your knowledge, this exploration of "2 squared" promises to enlighten and inspire.
What Does It Mean to Square a Number?
To understand "2 squared," we first need to grasp the concept of squaring a number. Squaring a number involves multiplying it by itself. In the case of 2, squaring it means performing the calculation:
- 2 x 2 = 4
This operation can be represented mathematically as 2² = 4, where the "²" symbolizes that the number is being squared. Squaring is a fundamental operation in mathematics, and it serves as a building block for more advanced concepts.
How is Squaring Used in Various Mathematical Fields?
Squaring numbers, such as "2 squared," plays an essential role in various mathematical disciplines, including:
- Algebra: In algebra, squaring is often used to solve equations and simplify expressions.
- Geometry: The area of a square can be calculated using squaring; for example, the area of a square with a side length of 2 is 2² = 4.
- Statistics: Squaring deviations from the mean is a crucial step in calculating variance.
- Calculus: Squaring functions is common in calculus to find areas under curves.
Why is Squaring Important in Real Life?
Squaring numbers has practical applications beyond the classroom. Here are a few examples:
- Construction: Understanding the area of spaces helps in planning and building.
- Finance: Squaring can help in calculating compound interest in investments.
- Physics: Squared terms often appear in equations related to motion and energy.
What is the Historical Context of Squaring Numbers?
The concept of squaring numbers dates back to ancient civilizations. The Babylonians and Egyptians utilized squaring in their mathematical calculations, laying the groundwork for future mathematical advancements. Over the centuries, scholars like Euclid and later mathematicians expanded on these ideas, leading to the formalization of squaring as we understand it today.
Are There Any Interesting Facts About Squaring Numbers?
Indeed, there are many intriguing aspects of squaring. Here are a few:
- Squaring a negative number results in a positive number, which is a fundamental property in mathematics.
- The number 0 squared is still 0, illustrating that squaring does not change the value of zero.
- Perfect squares, numbers that are squares of integers, have unique properties in number theory.
How Do We Use Squaring in Technology and Science?
In the fields of technology and science, squaring is crucial in various calculations. For example:
- In computer graphics, squaring is used to determine pixel density and image resolution.
- In physics, squaring velocity is essential in calculating kinetic energy.
- In data analysis, squaring differences from a mean helps in computing standard deviation and variance.
What Are the Educational Benefits of Learning About Squaring?
Understanding squaring and its applications can enhance mathematical proficiency in students. It fosters critical thinking and problem-solving skills, as students learn to apply squaring in various contexts. By mastering the concept of "2 squared," learners can build a strong foundation for more complex mathematical concepts, paving the way for success in advanced studies.
Can Squaring Be Fun and Engaging for Students?
Absolutely! There are numerous ways to make learning about squaring enjoyable:
- Interactive games that involve squaring numbers.
- Real-world projects that require measuring areas.
- Creative activities like art projects involving squares and geometric patterns.
How Can Parents and Educators Support Learning About Squaring?
Parents and educators can play a vital role in supporting the learning of squaring concepts:
- Encouraging hands-on activities that incorporate squaring.
- Providing resources like books and online tutorials that explain squaring in various contexts.
- Collaborating with students on projects that involve squaring and its applications.
In conclusion, "2 squared" serves as a gateway to understanding the broader concept of squaring numbers and its significance across multiple disciplines. By exploring its applications, historical context, and educational benefits, we can appreciate the value of squaring not just as a mathematical operation but as a crucial aspect of our daily lives and future endeavors.