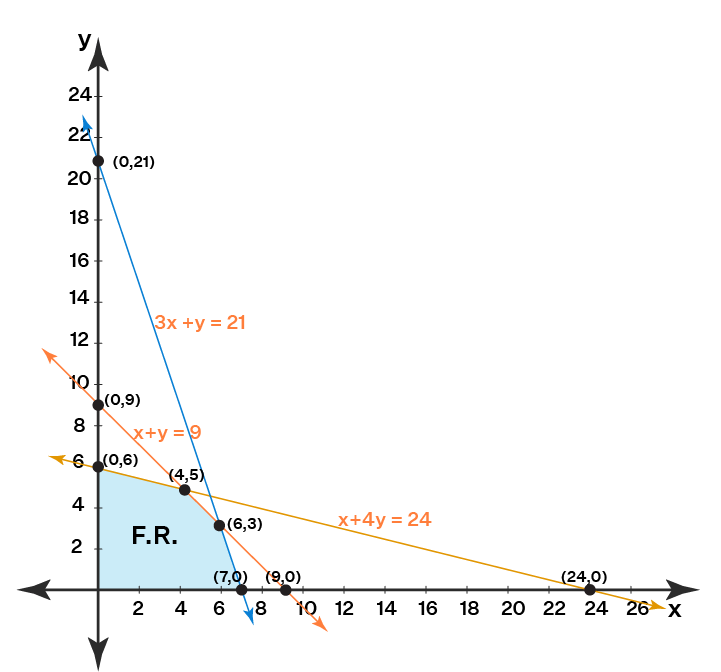
Linear programming is a mathematical technique used to optimize a particular outcome, given a set of constraints and linear relationships. It finds applications across various fields including economics, engineering, military operations, and transportation. By formulating problems into a system of linear equations and inequalities, linear programming enables decision-makers to determine the best course of action while maximizing or minimizing a specific objective.
At its core, linear programming revolves around the principles of linear equations. The beauty of this method lies in its ability to break down complex problems into simpler components, allowing for efficient analysis and solution finding. With the rise of technology, the applications of linear programming have expanded, paving the way for improved resource allocation and operational efficiency in various sectors. The intricate balance between constraints and objectives is what makes this mathematical approach so powerful.
In today's fast-paced world, the ability to make informed and optimal decisions is paramount. Linear programming serves as a vital tool for businesses and organizations aiming to enhance productivity and effectiveness. Whether it's determining the best mix of products to manufacture or optimizing a transportation schedule, the principles of linear programming are integral to achieving success in competitive environments.
What is Linear Programming?
Linear programming is a method for achieving the best outcome in a mathematical model whose requirements are represented by linear relationships. It is widely used for resource allocation, production scheduling, and many other optimization problems. The primary goal is to maximize or minimize a linear objective function while satisfying a set of linear constraints.
How Does Linear Programming Work?
The process of linear programming involves several steps:
- Defining the decision variables that will be used in the objective function and constraints.
- Formulating the objective function, which represents the goal of the optimization.
- Establishing the constraints that limit the available resources.
- Using graphical methods or simplex algorithms to find the optimal solution.
What Are the Key Components of Linear Programming?
Linear programming comprises three main components:
- Objective Function: This is the function that needs to be maximized or minimized.
- Decision Variables: These represent the choices available to the decision-maker.
- Constraints: These are the limitations or requirements that must be satisfied in the optimization process.
What Are the Applications of Linear Programming?
Linear programming has a wide range of applications across different industries:
- Manufacturing: Optimize production processes to minimize costs and maximize output.
- Transportation: Determine the most efficient routing of vehicles to minimize travel time and costs.
- Finance: Allocate investment portfolios efficiently to maximize returns.
- Supply Chain Management: Optimize inventory levels and distribution strategies.
What Are Some Real-World Examples of Linear Programming?
There are numerous real-world scenarios where linear programming has proven invaluable:
- Airlines utilize linear programming to optimize flight schedules and crew assignments.
- Retail companies apply linear programming to manage inventory and maximize sales.
- Energy companies use this technique to allocate resources effectively and reduce costs.
How Can Linear Programming Benefit Businesses?
Businesses can significantly benefit from implementing linear programming in various ways:
- Improved decision-making through data-driven analysis.
- Enhanced resource allocation leading to cost savings.
- Increased operational efficiency by optimizing processes.
- Greater competitiveness by adapting quickly to market changes.
What Are the Limitations of Linear Programming?
While linear programming is a powerful tool, it does have its limitations:
- Assumes linearity, which may not always be the case in real-world scenarios.
- Can become complex when dealing with large datasets or multiple variables.
- Does not account for uncertainties or fluctuations in data.
What is the Future of Linear Programming?
The future of linear programming is promising with advancements in technology and data analytics:
- Integration with artificial intelligence and machine learning to enhance predictive capabilities.
- Development of more sophisticated algorithms for improved efficiency.
- Increased use in real-time decision-making processes across industries.
Conclusion: The Value of Linear Programming in the Modern World
In conclusion, linear programming is an essential tool that facilitates optimal decision-making in various fields. Its ability to streamline processes, minimize costs, and allocate resources effectively makes it a cornerstone of modern operations. As technology continues to evolve, the applications and methodologies of linear programming will only expand, further cementing its place as a critical asset for businesses and organizations worldwide.